Bevor überhaupt mit der Erstellung des Modells begonnen werden konnte, musste ich die Größe der Laterne in den Maßstab 1:200 umrechnen.
Das ergab bei einer originalen Höhe von 24 m auf meinen Maßstab umgerechnet 12 cm.Zur besseren Visualisierung von Größe, Form und Aussehen der Laterne, fertigte ich zuallererst, ähnlich wie bei der Kuppel an sich, ein Grobmodell an.
Der erste Schritt war hierbei die Erstellung der unteren Scheibe, die aus einem äußeren und inneren Ring bestand und deren Zweck es war, als Schablone für die späteren Streben zu dienen, die an den Seiten angeordnet werden mussten. Das Problem der unteren Scheibe stellte die Tatsache dar, dass es dafür keinerlei Maße gab.
Ich besaß lediglich ein sehr genaues Foto der Laterne an dem ich mich von nun an orientieren musste. Da dieses Foto natürlich nicht im Maßstab 1:200 existierte, war meine erste Aufgabe die Maße des Fotos in meinen Maßstab umzurechnen.
Dabei ging ich folgendermaßen vor:Ich wusste, dass die 24 m der Laterne in meinem Maßstab 12 cm entsprachen auf dem Bild jedoch 15 cm waren.
Indem ich nun 12 cm durch 15 cm dividierte erhielt ich den Umrechnungsfaktor, der 0,8 betrug. Mit Hilfe dieses Faktors konnte ich von nun an alle sichtbaren Maße aus dem Bild abmessen und durch Multiplikation mit 0,8 in meinen Maßstab umrechnen.
Den nächsten Schritt des Modells stellte er Oktogonale Korpus der Laterne dar. Der gesamte Durchmesser war geben, weshalb ich nur noch die Breite einer einzelnen Rechteckfläche des Oktagons herausfinden musste.
Diese Breite bestimmte ich über ein zeichnerisches Verfahren. Ich konstruierte die acht Winkelhalbierende des Kreises, die jeweils im Winkel von 45° zueinander standen und maß daraufhin die Breite aus der Zeichnung ab.
Die Dachbodenplatte zwischen dem Korpus und dem pyramidalen Dach fertigte ich nach dem gleichen Prinzip, wie die untere Scheibe an. Die Platte entsprach dem inneren Ring der Scheibe, war aber etwas größer und oktogonal geformt.
Die Maße des Laternendachs ermittelte ich rechnerisch über den Satz des Pythagoras, welcher besagt, dass die beiden Kathetenquadrate exakt dem Flächeninhalt des Hypotenusenquadrats entsprechen.
Gegebene Größen waren einerseits die Höhe des Dachs und andererseits dessen Durchmesser. Indem ich den Radius durch 2 dividierte, war es mir möglich, das gleichschenklige Dreieck in ein rechtwinkliges umzuwandeln auf der der Satz des Pythagoras anwendbar war. Die gesuchte Größe, die Länge der Hypotenuse, entsprach dem Radius eines fiktiven Kreises aus dem sich das Laternendach zusammensetzte.
Der Radius stellte außerdem die schräge Seite des Laternendaches dar.
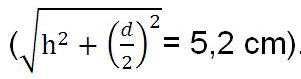 Nachdem ich die Wurzel aus der Höhe im Quadrat addiert mit dem halben Durchmesser im Quadrat gezogen hatte, erhielt ich den entsprechenden Radius, der 5,2 cm betrug.
Nachdem ich die Wurzel aus der Höhe im Quadrat addiert mit dem halben Durchmesser im Quadrat gezogen hatte, erhielt ich den entsprechenden Radius, der 5,2 cm betrug.Die stark verschnörkelten und verzierten Formen der Laterne stellte ich in einer abstrahierten Form dar. Das betraf vor allem die Dachstreben, für welche ich dicken Architektenkarton verwendete, der sich einigermaßen halbrund feilen ließ. Noch aufwendiger waren die Dachballustraden, die ich als Rechteck mit aufgesetztem Halbkreis, sowie kleinen Kunststoffstäben mit Kügelchen darstellte.
Erst nach diesen Vorarbeiten begann ich mit der Konstruktion des richtigen Modells der Laterne. Die Schritte waren dieselben, wurden aber in viel exakterer Weise und mit geeignetem und festerem Material angefertigt.
Den Abschluss der Laterne stellte die goldene Kugel mit dem goldenen Kreuz dar.
Nachdem ich das Kreuz zuerst aus Pappe ausgeschnitten hatte, entschied ich mich aber, der plastischen Wirkung wegen, dafür, es stattdessen aus Streichhölzern zu erstellen. Durch Besprühen mit einem Goldspray erhielt es die gewünschte Farbe.
